a side-by-side reference sheet
arithmetic and logic | strings | dates and time | multidimensional arrays | tuples, dictionaries, sequences | functions
execution control | environment and i/o | libraries and modules | reflection
vectors | matrices | statistics | distributions | data sets | univariate charts | bivariate charts | trivariate charts | contact
| fortran (1957) | matlab (1984) | r (2000) | numpy (2005) | |
|---|---|---|---|---|
| version used | GNU Fortran 4.5 (Fortran 95) | Octave 3.2 | 2.6 | Python 2.7 NumPy 1.6 SciPy 0.10 Matplotlib 1.0 |
| implicit prologue | none | none | none | import sys, os, re, math import numpy as np import scipy as sp import scipy.stats as stats import matplotlib as mpl import matplotlib.pyplot as plt |
| get version | $ gfortran --version | $ octave --version | $ r --version | sys.version np.__version__ sp.__version__ mpl.__version__ |
| command line repl | none | $ octave | $ r | $ python |
| interpreter |
none | $ octave foo.m | $ r -f foo.r | $ python foo.py |
| compiler |
$ gfortran foo.f90 -o foo | none | none | none |
| statement separator | newline when a line ends with & the statement continues on the following line |
; or newline | ; or sometimes newline | newline or ; newlines not separators inside (), [], {}, triple quote literals, or after backslash: \ |
| block delimiters | program end program function end function subroutine end subroutine if then elseif then else endif do while end do do end do |
function endfunction if elseif else endif while endwhile do until for endfor |
{ } | offside rule |
| assignment | i = 3 | i = 3 | i = 3 i <- 3 3 -> i assign("i",3) |
i = 3 |
| compound assignment operators: arithmetic, string, logical | none | MATLAB has no compound assignment operators. Octave has these: += -= *= /= none none **= or ^= none none &= |= none |
none | # do not return values: += -= *= /= //= %= **= += *= &= |= ^= |
| increment and decrement operator | none | ++x --x x++ x-- |
none | none |
| to-end-of-line comment | i = 1 + 1 ! addition | 1 + 1 % addition Octave only: 1 + 1 # addition |
1 + 1 # addition | 1 + 1 # addition |
| null | only used in place of numeric values: NA |
NA NULL | None | |
| null test | isna(v) true for '', []: isnull(v) |
is.na(v) is.null(v) |
v == None v is None |
|
| undefined variable access | variables must be declared under implicit none | raises error | raises error | raises NameError |
| variable types | integer real complex character logical | |||
| variable declaration | integer :: n real :: x = 3.7 |
none | none | none |
| are identifiers case sensitive | no; Fortran 77 and earlier required all caps | yes | yes | yes |
| arithmetic and logic | ||||
| fortran | matlab | r | numpy | |
| true and false |
.true. .false. | 1 0 true false | TRUE FALSE T F | True False |
| falsehoods | .false. no implicit conversion of values to booleans |
false 0 0.0 matrices evaluate to false unless nonempty and all entries evaluate to true |
FALSE F 0 0.0 matrices evaluate to value of first entry; string in boolean context causes error |
False None 0 0.0 '' [] {} |
| logical operators | .and. .or. .not. .eqv. .neqv. | ~true | (true & false) Optional negation operator in Octave: ! short-circuit operators: && || |
!TRUE | (TRUE & FALSE) short-circuit operators: && || |
and or not |
| conditional expression | none | none | (if (x > 0) x else -x) ifelse(x > 0, x, -x) |
x if x > 0 else -x |
| convert from string, to string | 7 + str2num('12') 73.9 + str2num('.037') horzcat('value: ', num2str(8)) |
7 + as.integer("12") 73.9 + as.double(".037") paste("value: ", toString("8")) |
7 + int('12') 73.9 + float('.037') 'value: ' + str(8) |
|
| comparison operators | == /= > < >= <= | == ~= > < >= <= Optional inequality operator in Octave: != |
== != > < >= <= | == != > < >= <= |
| arithmetic operators | + - * none / mod(n, divisor) ** | + - * / none mod(n, divisor) ** or ^ | + - * / ? ? ** or ^ | + - * / // % ** |
| integer division |
13 / 5 | fix(13 / 5) | as.integer(13 / 5) | 13 // 5 |
| float division |
real(13) / 5 | 13 / 5 | 13 / 5 | float(13) / 5 |
| arithmetic functions | sqrt exp log sin cos tan asin acos atan atan2 | sqrt exp log sin cos tan asin acos atan atan2 | sqrt exp log sin cos tan asin acos atan atan2 | math.sqrt math.exp math.log math.sin math.cos math.tan math.asin math.acos math.atan math.atan2 |
| arithmetic truncation | int(3.7) ?? ceiling(3.7) floor(3.7) |
fix round ceil floor | as.integer round ceiling floor | int(x) int(round(x)) math.ceil(x) math.floor(x) |
| arithmetic decomposition | abs(-3.7) sign(1.0, -3.7) real(z) imag(z) atan2(imag(z), real(z)) |
abs sign real imag arg | abs sign Re Im Arg | import cmath abs(-3.7) math.copysign(1, -3.7) z.real z.imag cmath.polar(z)[1] |
| closure of integers under division | integers | floats | floats | integers |
| integer overflow | modular arithmetic | becomes float; largest representable integer in the variable intmax | becomes float; largest representable integer in the variable .Machine$integer.max | becomes arbitrary length integer of type long |
| float overflow |
Inf | Inf | raises OverflowError | |
| float limits |
eps realmax realmin |
.Machine$double.eps .Machine$double.xmax .Machine$double.xmin |
np.finfo(np.float64).eps np.finfo(np.float64).max np.finfo(np.float64).min |
|
| 1/0 | real :: x = 0.0 ! compiler error: 1.0 / 0.0 ! +Infinity: 1.0 / x |
Inf | Inf | raises ZeroDivisionError |
| sqrt(-2) | real :: x = -2.0 complex :: z = (-2.0, 0.0) ! compiler error: sqrt(-2.0) ! NaN: sqrt(x) ! (0.000, 1.414) sqrt(z) |
sqrt(-2) 0.00000 + 1.41421i |
sqrt(-2) NaN sqrt(-2+0i) 0+1.414214i |
# raises ValueError: math.sqrt(-2) # returns 1.41421j: import cmath cmath.sqrt(-2) |
| complex numbers | (0.0, 1.0) (0.0, 2.0) (0.0, 3.0) |
i 2i 3i |
1i 2i 3i |
1j 2j 3j |
| random integer |
floor(100*rand) | floor(100*runif(1)) | np.random.randint(0,100) | |
| random float |
rand(0) | rand | runif(1) | np.random.rand() |
| setting seed |
rand('state', 17) | set.seed(17) | np.random.seed(17) | |
| result of not seeding | the same after each run | seeded using operating system entropy | seeded using current time | on Unix reads seed from /dev/random |
| strings | ||||
| fortran | matlab | r | numpy | |
| literal | 'don''t say "no"' "don't say ""no""" |
'don''t say "no"' Octave also has double quoted strings: "don't say \"no\"" |
"don't say \"no\"" 'don\'t say "no"' |
'don\'t say "no"' "don't say \"no\"" r"don't " r'say "no"' |
| newline in literal |
"lorem" // achar(10) // "ipsum" | no; use \n escape | yes | no |
| literal escapes | none | \\ \" \' \0 \a \b \f \n \r \t \v | \\ \" \' \a \b \f \n \r \t \v \ooo | single and double quoted: \newline \\ \' \" \a \b \f \n \r \t \v \ooo \xhh |
| character access |
"hello"(1:1) | 'hello'(1) | substr("hello",1,1) | 'hello'[0] |
| chr and ord | achar(65) iachar('A') |
char(65) toascii('A') |
intToUtf8(65) utf8ToInt("A") |
chr(65) ord('A') |
| length |
len("hello") | length('hello') | nchar("hello") | len('hello') |
| concatenate | 'one ' // 'two ' // 'three' | horzcat('one ', 'two ', 'three') | paste("one ", "two ", "three") | 'one ' + 'two ' + 'three' literals, but not variables, can be concatenated with juxtaposition: 'one ' "two " 'three' |
| replicate | character(len=80) :: hbar hbar = repeat('-', 80) |
hbar = repmat('-', 1, 80) | hbar = paste(rep('-',80),collapse='') | hbar = '-' * 80 |
| index of substring | counts from one, returns zero if not found index("hello", "el") |
counts from one, returns zero if not found index('hello', 'el') |
counts from one, returns -1 if not found regexpr("el", "hello") |
counts from zero, raises ValueError if not found: 'hello'.index('el') |
| extract substring |
"hello"(1:4) | substr('hello',1,4) | substr("hello",1,4) | 'hello'[0:4] |
| split | none | returns tuple: strsplit('foo,bar,baz',',') |
strsplit('foo,bar,baz', ',') | 'foo,bar,baz'.split(',') |
| join | paste("foo", "bar", "baz", sep=",") paste(c('foo','bar','baz'), collapse=',') |
','.join(['foo','bar','baz']) | ||
| trim | ?? adjustl(' foo') trim('foo ') |
strtrim(' foo ') ?? deblank('foo ') |
gsub("(^[\n\t ]+|[\n\t ]+$)", "", " foo ") sub("^[\n\t ]+", "", " foo") sub("[\n\t ]+$", "", "foo ") |
' foo '.strip() ' foo'.lstrip() 'foo '.rstrip() |
| case manipulation | none | lower('FOO') upper('foo') |
tolower("FOO") toupper("foo") |
'foo'.upper() 'FOO'.lower() 'foo'.capitalize() |
| sprintf | character(len=100) :: s write(s,'(A A F9.3 I9)') 'foo', ':', 2.2, 7 |
sprintf('%s: %.3f %d', 'foo', 2.2, 7) | sprintf("%s: %.3f %d", "foo", 2.2, 7) | '%s: %.3f %d' % ('foo',2.2,7) |
| regex test | none | regexp('hello','^[a-z]+$') regexp('hello','^\S+$') |
regexpr("^[a-z]+$", "hello") > 0 regexpr('^\\S+$', "hello",perl=T) > 0 |
re.search('^[a-z]+$', 'hello') re.search('^\S+$', 'hello') |
| regex substitution | none | regexprep('foo bar bar','bar','baz','once') regexprep('foo bar bar','bar','baz') |
sub('bar','baz','foo bar') gsub('bar','baz','foo bar bar') |
rx = re.compile('bar') s = rx.sub('baz', 'foo bar', 1) s2 = rx.sub('baz', 'foo bar bar') |
| dates and time | ||||
| fortran | matlab | r | numpy | |
| current date/time | GNU Fortran: t = time() |
t = now | t = as.POSIXlt(Sys.time()) | |
| date/time type | integer representing seconds since Jan 1, 1970 UTC | floating point number representing days since year 0 in the Gregorian calendar | POSIXlt | |
| date/time difference type | integer representing seconds | floating point number representing days | a difftime object which behaves like a floating point number representing seconds | |
| get date parts | integer::values(9); integer year,mon,day call ltime(t, values) year = values(6) + 1900 mon = values(5) + 1 day = values(4) |
datevec(t)(1) datevec(t)(2) datevec(t)(3) |
t$year + 1900 t$mon + 1 t$mday |
|
| get time parts | integer::values(9) integer hour,min,sec call ltime(t, values) hour = values(3) min = values(2) sec = values(1) |
datevec(t)(4) datevec(t)(5) datevec(t)(6) |
t$hour t$min t$sec |
|
| build date/time from parts | none | t = datenum([2011 9 20 23 1 2]) | t = as.POSIXlt(Sys.time()) t$year = 2011 - 1900 t$mon = 9 - 1 t$mday = 20 t$hour = 23 t$min = 1 t$sec = 2 |
|
| convert to string |
ctime(t) | datestr(t) | print(t) | |
| strptime | none | t = datenum('2011-09-20 23:01:02', 'yyyy-mm-dd HH:MM:SS') |
t = strptime('2011-09-20 23:01:02', '%Y-%m-%d %H:%M:%S') |
|
| strftime |
none | datestr(t, 'yyyy-mm-dd HH:MM:SS') | format(t, format='%Y-%m-%d %H:%M:%S') | |
| multidimensional arrays | ||||
| fortran | matlab | r | numpy | |
| array literal | integer::a(3) = (/ 1, 2, 3 /) | [1,2,3] commas are optional: [1 2 3] |
c(1,2,3) | np.array([1,2,3]) |
| 2d array literal | integer::a(2,2) = & reshape((/ 1, 2, 3, 4 /), & (/ 2, 2 /)) |
[1,2;3,4] spaces and newlines can replace commas and semicolons: [1 2 3 4] |
array(c(1,2,3,4),dim=c(2,2)) | np.array([[1,2],[3,4]]) |
| 3d array literal | A = [1,2;3,4] A(:,:,2) = [5,6;7,8] |
array(c(1,2,3,4,5,6,7,8),dim=c(2,2,2)) | np.array([[[1,2],[3,4]],[[5,6],[7,8]]]) | |
| must arrays be homogeneous | yes | yes | yes | yes |
| array data type | depends on declaration; no run time type inspection | always numeric | class(c(1,2,3)) a = array(c(1,2,3)) class(c(a)) |
np.array([1,2,3]).dtype |
| data types permitted in arrays | any but type must be declared | numeric | boolean, numeric, string | np.bool, np.int64, np.float64, np.complex128, and others |
| array element access | ! indices start at one integer::a(3) a = (/ 1, 2, 3 /) a(1) |
indices start at one: [1 2 3](1) |
indices start at one: c(1,2,3)[1] |
indices start at zero: a = np.array([1,2,3]) a[0] |
| index of array element | which(c(7,8,9)==9) | |||
| array slice | ! can't slice literal int::a1(3),a2(2) a1 = (/1,2,3/) a2 = a1(1:2) |
[1 2 3](1:2) | c(1,2,3)[1:2] | np.array([1,2,3])[0:2] |
| integer array as index | [1 2 3]([1,3,3]) | c(1,2,3)[c(1,3,3)] | np.array([1,2,3])[[0,2,2]] | |
| logical array as index | [1 2 3]([true false true]) | c(1,2,3)[c(T,F,T)] | np.array([1,2,3])[[True,False,True]] | |
| array length |
size((/ 1, 2, 3 /)) | length([1 2 3]) | length(c(1,2,3)) | len(np.array([1,2,3])) |
| multidimensional array size | length(dim(a)) dim(a) |
a.ndim a.shape |
||
| array concatenation | cat(2, [1 2 3], [4 5 6]) horzcat([1 2 3], [4 5 6]) |
append(c(1,2,3),c(4,5,6)) | a1 = np.array([1,2,3]) a2 = np.array([4,5,6]) np.concatenate([a1,a2]) |
|
| sort | a = [3 1 4 2] a = sort(a) |
a = c(3,1,4,2) a = sort(a) |
a = np.array([3,1,4,2]) a.sort() |
|
| map | arrayfun( @(x) x*x, [1 2 3]) | sapply(c(1,2,3), function (x) { x * x}) | a = np.array([1,2,3]) np.vectorize(lambda x: x*x)(a) |
|
| filter | v = [1 2 3] v(v > 2) |
v = c(1,2,3) v[v > 2] |
v = np.array([1,2,3]) a = [x for x in v if x > 2] np.array(a) |
|
| sample w/o replacement | x = c(3,7,5,12,19,8,4) sample(x, 3) |
from random import sample sample([3,7,5,12,19,8,4], 3) |
||
| tuples, dictionaries, sequences | ||||
| fortran | matlab | r | numpy | |
| tuple literal |
none | tup = {1.7, 'hello', [1 2 3]} | tup = list(1.7,"hello",c(1,2,3)) | tup = (1.7, "hello", [1,2,3]) |
| tuple element access | none | tup{1} | tup[[1]] | tup[0] |
| tuple length |
none | length(tup) | length(tup) | len(tup) |
| dictionary literal |
none | d = struct('n',10,'avg',3.7,'sd',0.4) | d = list(n=10, avg=3.7, sd=0.4) | d = {'n':10, 'avg':3.7, 'sd':0.4} |
| dictionary lookup |
none | d.n | d$n | d['n'] |
| range | 1:100 | 1:100 seq(1,100) |
range(1, 101) | |
| arithmetic sequence of integers with difference 10 | 0:10:100 | seq(0,100,10) | range(0, 101, 10) | |
| arithmetic sequence of floats with difference 0.1 | 0:0.1:10 | seq(0,10,0.1) | [0.1*x for x in range(0,101)] 3rd arg is length of sequence, not step size: sp.linspace(0, 10, 100) |
|
| functions | ||||
| fortran | matlab | r | numpy | |
| definition | integer function add(n, m) integer, intent(in) :: n integer, intent(in) :: m add = n + m end function add |
function add(a,b) a+b endfunction |
add = function(a,b) {a + b} | |
| invocation |
add(3, 7) | add(3, 7) | add(3, 7) | |
| return value | assign to implicit variable with same name as function; can use return statement to terminate function execution | how to declare a return variable: function retvar = add(a,b) retvar = a + b endfunction the return value is the value assigned to the return variable if one is defined; otherwise it's the last expression evaluated. |
return argument or last expression evaluated. NULL if return called without an argument. | |
| function value | none; function pointers added in Fortran 2003 | @add | add | |
| anonymous function | none; see above | @(a,b) a+b | function(a,b) {a+b} | |
| missing argument | set to zero | raises error if code with the parameter that is missing an argument is executed | raises error | |
| extra argument |
ignored | ignored | raises error | |
| default argument | real function mylog(x, base) real :: x real, optional :: base if (present(base)) then mylog = log(x) / log(base) else mylog = log(x) / log(10.0) endif end function mylog |
function mylog(x, base=10) log(x) / log(base) endfunction |
mylog = function(x,base=10) { log(x) / log(base) } |
|
| variable number of arguments | none | function s = add(varargin) if nargin == 0 s = 0 else r = add(varargin{2:nargin}) s = varagin{1} + r endif endfunction |
add = function (...) { a = list(...) if (length(a) == 0) return(0) s = 0 for(i in 1:length(a)) { s = s + a[[i]] } return(s) } |
|
| execution control | ||||
| fortran | matlab | r | numpy | |
| if | if (n == 0) then write(*,*) 'no hits' elseif (n == 1) then write(*,*) 'one hit' else write(*,*) n, 'hits' endif |
if (x > 0) printf('positive\n') elseif (x < 0) printf('negative\n') else printf('zero\n') endif |
if (x > 0) { print('positive') } else if (x < 0) { print('negative') } else { print('zero') } |
if x > 0: print('positive') elif x < 0: print('negative') else: print('zero') |
| while | n = 1 do while ( n < 10 ) write(*,*) n n = n + 1 end do |
i = 0 while (i < 10) i++ printf('%d\n', i) endwhile |
while (i < 10) { i = i + 1 print(i) } |
while i < 10: i += 1 print(i) |
| for | do n = 1, 10, 1 write(*,*) n end do |
for i = 1:10 printf('%d\n', i) endfor |
for (i in 1:10) { print(i) } |
for i in range(1,11): print(i) |
| break/continue |
exit cycle | break continue | break next | break continue |
| raise exception | write(0, "failed") call exit(-1) |
error('%s', 'failed') | stop('failed') | raise Exception('failed') |
| handle exception | none | try error('failed') catch printf('%s\n', lasterr()) end_try_catch |
tryCatch( stop('failed'), error=function(e) print(message(e))) |
try: raise Exception('failed') except Exception as e: print(e) |
| finally block | none | unwind_protect if ( rand > 0.5 ) error('failed') endif unwind_protect_cleanup printf('cleanup') end_unwind_protect |
risky = function() { if (runif(1) > 0.5) { stop('failed') } } tryCatch( risky(), finally=print('cleanup')) |
|
| environment and i/o | ||||
| fortran | matlab | r | numpy | |
| write to stdout | write(*,*) 'hello' | printf('hello\n') | print('hello') | |
| read entire file into string or array | con = file("/etc/hosts", "r") a = readLines(con) |
|||
| redirect to file | sink("foo.txt") | |||
| libraries and modules | ||||
| fortran | matlab | r | numpy | |
| load library | % if installed as Octave package: pkg load foo |
require("foo") or library("foo") |
import foo | |
| list loaded libraries | none | none | search() | dir() |
| library search path | path() addath('~/foo') rmpath('~/foo') |
.libPaths() | sys.path | |
| source file |
none | source('foo.m') | source("foo.r") | none |
| install package | none | % installs packages downloaded from % Octave-Forge in Octave: pkg install foo-1.0.0.tar.gz |
install.packages("ggplot2") | $ pip install scipy |
| list installed packages | none | pkg list | library() | $ pip freeze |
| reflection | ||||
| fortran | matlab | r | numpy | |
| data type | none, but variable type must be declared | class(x) | class(x) | type(x) |
| attributes | none, and Fortran 95 does not have objects | if x is an object value: x |
attributes(x) | [m for m in dir(x) if not callable(getattr(o,m))] |
| methods | none | note that most values are not objects: methods(x) |
none; objects are implemented by functions which dispatch based on type of first arg | [m for m in dir(x) if callable(getattr(o,m))] |
| variables in scope | none | who() | objects() | dir() |
| undefine variable |
none | clear('x') | rm(v) | del(x) |
| eval |
none | eval('1+1') | eval(parse(text='1+1')) | eval('1+1') |
| function documentation | none | help tan | help(tan) ?tan |
math.tan.__doc__ |
| list library functions | none | none | ls("package:moments") | dir(stats) |
| search documentation | none | not in Octave: docsearch tan |
??tan | $ pydoc -k tan |
| vectors | ||||
| fortran | matlab | r | numpy | |
| vector literal | same as array | same as array | same as array | same as array |
| element-wise arithmetic operators | + - * / | + - .* ./ | + - * / | + - * / |
| result of vector length mismatch | compilation error | raises error | values in shorter vector are recycled; warning if one vector is not a multiple length of the other | raises ValueError |
| scalar multiplication | 3 * (/1,2,3/) (/1,2,3/) * 3 |
3 * [1,2,3] [1,2,3] * 3 |
3 * c(1,2,3) c(1,2,3) * 3 |
3 * np.array([1,2,3]) np.array([1,2,3]) * 3 |
| dot product | dot_product((/1,1,1/),(/2,2,2/)) | dot([1,1,1], [2,2,2]) | c(1,1,1) %*% c(2,2,2) | v1 = np.array([1,1,1]) v2 = np.array([2,2,2]) np.dot(v1,v2) |
| cross product | cross([1,0,0], [0,1,0]) | v1 = np.array([1,0,0]) v2 = np.array([0,1,0]) np.cross(v1,v2) |
||
| norms | norm([1,2,3], 1) norm([1,2,3], 2) norm([1,2,3], Inf) |
vnorm = function(x, t) { norm(matrix(x, ncol=1), t) } vnorm(c(1,2,3), "1") vnorm(c(1,2,3), "E") vnorm(c(1,2,3), "I") |
v = np.array([1,2,3]) np.linalg.norm(v, 1) np.linalg.norm(v, 2) np.linalg.norm(v, np.inf) |
|
| matrices | ||||
| fortran | matlab | r | numpy | |
| literal or constructor | column contiguous: integer::A(2,2) = & reshape((/ 1, 3, 2, 4 /), & (/ 2, 2 /)) integer::B(2,2) = & reshape((/ 4, 2, 3, 1 /), & (/ 2, 2 /)) |
row contiguous: A = [1,2;3,4] B = [4 3 2 1] |
column contiguous: A = matrix(c(1,3,2,4), 2, 2) B = matrix(c(4,2,3,1), nrow=2) |
row contiguous: A = np.matrix([[1,2],[3,4]]) B = np.matrix([[4,3],[2,1]]) |
| zero, identity, ones, diagonal matrix | zeros(3,3) or zeros(3) eye(3) ones(3,3) or ones(3) diag([1,2,3]) |
matrix(0,3,3) diag(3) matrix(1,3,3) diag(c(1,2,3)) |
||
| dimensions | rows(A) columns(A) |
dim(A)[1] dim(A)[2] |
||
| element access | A(1,1) | A[1,1] | A[0,0] | |
| row access | A(1,1:2) | A[1,] | A[0] | |
| column access | A(1:2,1) | A[,1] | ||
| submatrix access | C = [1,2,3;4,5,6;7,8,9] C(1:2,1:2) |
C = matrix(seq(1,9),3,3,byrow=T) C[1:2,1:2] |
||
| scalar multiplication | 3 * A A * 3 also: 3 .* A A .* 3 |
3 * A A * 3 |
3 * A A * 3 |
|
| element-wise operators | .+ .- .* ./ | + - * / | + - np.multiply() np.divide() | |
| multiplication | matmul(A, B) | A * B | A %*% B | A * B |
| power | A ** 3 | |||
| kronecker product | kron(A,B) | kronecker(A,B) | np.kron(A, B) | |
| comparison | all(all(A==B)) any(any(A!=A)) |
all(A==B) any(A!=B) |
||
| norms | norm(A,1) norm(A,2) norm(A,Inf) norm(A,'fro') |
norm(A,"1") ?? norm(A,"I") norm(A,"F") |
||
| transpose | transpose(A) A' |
t(A) | A.transpose() | |
| conjugate transpose | A = [1i,2i;3i,4i] A' |
A = matrix(c(1i,2i,3i,4i), nrow=2, byrow=T) Conj(t(A)) |
A = np.matrix([[1j,2j],[3j,4j]]) A.conj().transpose() |
|
| inverse | inv(A) | solve(A) | np.linalg.inv(A) | |
| determinant | det(A) | det(A) | np.linalg.det(A) | |
| trace | trace(A) | sum(diag(A)) | A.trace() | |
| eigenvalues | eig(A) | eigen(A)$values | np.linalg.eigvals(A) | |
| eigenvectors | [evec,eval] = eig(A) evec(1:2) evec(3:4) |
eigen(A)$vectors | np.linalg.eig(A)[1] | |
| system of equations | A \ [2;3] | solve(A,c(2,3)) | np.linalg.solve(A, [2,3]) | |
| statistics | ||||
| fortran | matlab | r | numpy | |
| first moment statistics | x = [1 2 3 8 12 19] sum(x) mean(x) |
x = c(1,2,3,8,12,19) sum(x) mean(x) |
x = [1,2,3,8,12,19] sp.sum(x) sp.mean(x) |
|
| second moment statistics | std(x, 1) var(x, 1) |
n = length(x) sd(x) * sqrt((n-1)/n) var(x) * (n-1)/n |
sp.std(x) sp.var(x) |
|
| second moment statistics for samples | std(x) var(x) |
sd(x) var(x) |
n = float(len(x)) sp.std(x) * math.sqrt(n/(n-1)) sp.var(x) * n/(n-1) |
|
| skewness | Octave uses sample standard deviation to compute skewness: skewness(x) |
install.packages('moments') library('moments') skewness(x) |
stats.skew(x) | |
| kurtosis | Octave uses sample standard deviation to compute kurtosis: kurtosis(x) |
install.packages('moments') library('moments') kurtosis(x) - 3 |
stats.kurtosis(x) | |
| nth moment and nth central moment | n = 5 moment(x, n) moment(x, n, "c") |
install.packages('moments') library('moments') n = 5 moment(x, n) moment(x, n, central=T) |
n = 5 ?? stats.moment(x, n) |
|
| mode | mode([1 2 2 2 3 3 4]) | samp = c(1,2,2,2,3,3,4) names(sort(-table(samp)))[1] |
stats.mode([1,2,2,2,3,3,4])[0][0] | |
| quantile statistics | min(x) median(x) max(x) ? |
min(x) median(x) max(x) quantile(x, prob=.90) |
min(x) sp.median(x) max(x) stats.scoreatpercentile(x, 90.0) |
|
| linear regression y = ax + b | x = [1 2 3] y = [2 4 7] [lsq, res] = polyfit(x, y, 1) a = lsq(1) b = lsq(2) y - (a*x+b) |
x = c(1,2,3) y = c(2,4,7) lsq = lm(y ~ x) a = lsq$coefficients[2] b = lsq$coefficients[1] lsq$residuals |
x = np.array([1,2,3]) y = np.array([2,4,7]) lsq = stats.linregress(x, y) a = lsq[0] b = lsq[1] y - (a*x+b) |
|
| bivariate statistiscs | x = [1 2 3] y = [2 4 7] cor(x, y) cov(x, y) |
x = c(1,2,3) y = c(2,4,7) cor(x, y) cov(x, y) |
x = [1,2,3] y = [2,4,7] stats.linregress(x, y)[2] ?? |
|
| distributions | ||||
| fortran | matlab | r | numpy | |
| binomial | binopdf(x, n, p) binocdf(x, n, p) binoinv(y, n, p) binornd(n, p) |
dbinom(x, n, p) pbinom(x, n, p) qbinom(y, n, p) rbinom(1, n, p) |
stats.binom.pmf(x, n, p) stats.binom.cdf(x, n, p) stats.binom.ppf(y, n, p) stats.binom.rvs(n, p) |
|
| poisson | poisspdf(x, lambda) poisscdf(x, lambda) poissinv(y, lambda) poissrnd(lambda) |
dpois(x, lambda) ppois(x, lambda) qpois(y, lambda) rpois(1, lambda) |
stats.poisson.pmf(x, lambda) stats.poisson.cdf(x, lambda) stats.poisson.ppf(y, lambda) stats.poisson.rvs(lambda, size=1) |
|
| normal | normpdf(x, mu, sigma) normcdf(x, mu, sigma) norminv(y, mu, sigma) normrnd(mu, sigma) |
dnorm(x, mu, sigma) pnorm(x, mu, sigma) qnorm(y, mu, sigma) rnorm(1, mu, sigma) |
stats.norm.pdf(x, mu, sigma) stats.norm.cdf(x, mu, sigma) stats.norm.ppf(y, mu, sigma) stats.norm.rvs(mu, sigma) |
|
| gamma | gampdf(x, k, theta) gamcdf(x, k, theta) gaminv(y, k, theta) gamrnd(k, theta) |
dgamma(x, k, scale=theta) pgamma(x, k, scale=theta) qgamma(y, k, scale=theta) rgamma(1, k, scale=theta) |
stats.gamma.pdf(x, k, scale=theta) stats.gamma.cdf(x, k, scale=theta) stats.gamma.ppf(y, k, scale=theta) stats.gamma.rvs(k, scale=theta) |
|
| exponential | exppdf(x, lambda) expcdf(x, lambda) expinv(y, lambda) exprnd(lambda) |
dexp(x, lambda) pexp(x, lambda) qexp(y, lambda) rexp(1, lambda) |
stats.expon.pdf(x, scale=1.0/lambda) stats.expon.cdf(x, scale=1.0/lambda) stats.expon.ppf(x, scale=1.0/lambda) stats.expon.rvs(scale=1.0/lambda) |
|
| chi-squared | chi2pdf(x, nu) chi2cdf(x, nu) chi2inv(y, nu) chi2rnd(nu) |
dchisq(x, nu) pchisq(x, nu) qchisq(y, nu) rchisq(1, nu) |
stats.chi2.pdf(x, nu) stats.chi2.cdf(x, nu) stats.chi2.ppf(y, nu) stats.chi2.rvs(nu) |
|
| beta | betapdf(x, alpha, beta) betacdf(x, alpha, beta) betainvf(y, alpha, beta) betarnd(alpha, beta) |
dbeta(x, alpha, beta) pbeta(x, alpha, beta) qbeta(y, alpha, beta) rbeta(1, alpha, beta) |
stats.beta.pdf(x, alpha, beta) stats.beta.cdf(x, alpha, beta) stats.beta.ppf(y, alpha, beta) stats.beta.pvs(alpha, beta) |
|
| uniform | unifpdf(x, a, b) unifcdf(x, a, b) unifinv(y, a, b) unifrnd(a, b) |
dunif(x, a, b) punif(x, a, b) qunif(y, a, b) runif(1, a, b) |
stats.uniform.pdf(x, a, b) stats.uniform.cdf(x, a, b) stats.uniform.ppf(y, a, b) stats.unifrom.rvs(a, b) |
|
| Student's t | dt(x, nu) pt(x, nu) qt(y, nu) rt(1, nu) |
stats.t.pdf(x, nu) stats.t.cdf(x, nu) stats.t.ppf(y, nu) stats.t.rvs(nu) |
||
| Snedecor's F | df(x, d1, d2) pf(x, d1, d2) qf(y, d1, d2) rf(1, d1, d2) |
stats.f.pdf(x, d1, d2) stats.f.cdf(x, d1, d2) stats.f.ppf(y, d1, d2) stats.f.rvs(d1, d2) |
||
| data sets | ||||
| r | ||||
| construct from arrays | gender, height, weight of some people in inches and lbs: sx = c("F","F","F","F","M","M") ht = c(69,64,67,66,72,70) wt = c(150,132,142,139,167,165) people = data.frame(sx, ht, wt) |
|||
| view in spreadsheet | can edit data, in which case return value of edit must be saved people = edit(people) |
|||
| list column names | names(people) | |||
| attach column names | copy columns into variables named sx, ht and wt: attach(people) |
|||
| detach column names | detach(people) | |||
| column access | vectors: people$ht people[,2] 1 column data set: people[2] |
|||
| row access | 1 row data set: people[1,] list: as.list(people[1,]) |
|||
| access sub data set | data set of first 3 rows with ht and wt columns reversed people[1:3,c(1,3,2)] |
|||
| access datum | datum in 1st row, 2nd column: people[1,2] |
|||
| sort rows of data set | people[order(people$ht),] | |||
| sort rows in descending order | people[order(-people$ht),] | |||
| map data set | convert to cm and kg: transform(people, ht=2.54*ht, wt=wt/2.2) |
|||
| filter data set | subset(people, ht > 66) people[people$ht > 66,] |
|||
| load from csv |
people = read.csv('/path/to.csv') | |||
| save as csv |
write.csv('/path/to.csv') | |||
| show built-in data sets | data() | |||
| load built-in data set | data(iris) | |||
| univariate charts | ||||
| matlab | r | matplotlib | ||
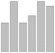 vertical bar chart vertical bar chart |
bar([7 3 8 5 5]) | cnts = c(7,3,8,5,5) names(cnts) = c("a","b","c","d","e") barplot(cnts) x = floor(6*runif(100)) barplot(table(x)) |
cnts = [7,3,8,5,5] plt.bar(range(0,len(cnts)), cnts) |
|
 horizontal bar chart |
barh([7 3 8 5 5]) | cnts = c(7,3,8,5,5) names(cnts) = c("a","b","c","d","e") barplot(cnts, horiz=T) |
cnts = [7,3,8,5,5] plt.barh(range(0,len(cnts)), cnts) |
|
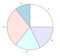 pie chart pie chart |
labels = {'a','b','c','d','e'} pie([7 3 8 5 5], labels) |
cnts = c(7,3,8,5,5) names(cnts) = c("a","b","c","d","e") pie(cnts) |
cnts = [7,3,8,5,5] labs = ['a','b','c','d','e'] plt.pie(cnts, labels=labs) |
|
 stacked dot chart stacked dot chart |
stripchart(floor(10*runif(50)), method="stack", offset=1, pch=19) |
|||
 stem-and-leaf plot |
generates an ascii chart: stem(20*rnorm(100)) |
|||
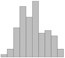 histogram histogram |
hist(randn(1,100),10) | hist(rnorm(100),breaks=10) | plt.hist(sp.randn(100), bins=range(-5,5)) |
|
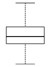 box-and-whisker plot box-and-whisker plot |
boxplot(rnorm(100)) boxplot(rnorm(100), rexp(100), runif(100)) |
plt.boxplot(sp.randn(100)) plt.boxplot([sp.randn(100), np.random.uniform(size=100), np.random.exponential(size=100)]) |
||
| set chart title | all chart functions except for stem accept a main parameter: boxplot(rnorm(100), main="boxplot example", sub="to illustrate options") |
plt.boxplot(sp.randn(100)) plt.title('boxplot example') |
||
| bivariate charts | ||||
| matlab | r | matplotlib | ||
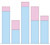 stacked bar chart |
d = [7 1; 3 2; 8 1; 5 3; 5 1] bar(d, 'stacked') |
d = matrix(c(7,1,3,2,8,1,5,3,5,1), nrow=2) labels = c("a","b","c","d","e") barplot(d,names.arg=labels) |
a1 = [7,3,8,5,5] a2 = [1,2,1,3,1] plt.bar(range(0,5), a1, color='r') plt.bar(range(0,5), a2, color='b') |
|
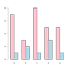 grouped bar chart |
d = [7 1; 3 2; 8 1; 5 3; 5 1] bar(d) |
d = matrix(c(7,1,3,2,8,1,5,3,5,1), nrow=2) labels = c("a","b","c","d","e") barplot(d,names.arg=labels,beside=TRUE) |
||
 scatter plot scatter plot |
plot(randn(1,50),randn(1,50),'+') | plot(rnorm(50), rnorm(50)) | plt.scatter(sp.randn(50), sp.randn(50)) |
|
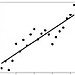 linear regression line linear regression line |
x = 0:20 y = 2 * x + rnorm(21)*10 o = lm(y ~ x) plot(y) lines(o$fitted.values) |
x = range(0,20) err = sp.randn(20)*10 y = [2*i for i in x] + err A = np.vstack([x,np.ones(len(x))]).T m, c = np.linalg.lstsq(A, y)[0] plt.scatter(x, y) plt.plot(x, [m*i + c for i in x]) |
||
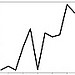 polygonal line plot polygonal line plot |
plot(1:20,randn(1,20)) | plot(1:20, rnorm(20), type="l") | plot(range(0,20), randn(20)) | |
 area chart area chart |
||||
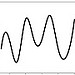 cubic spline cubic spline |
f = splinefun(rnorm(20)) x = seq(1,20,.1) plot(x,f(x),type="l") |
|||
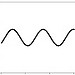 function plot function plot |
fplot(@sin, [-4 4]) | x = seq(-4,4,.01) plot(sin(x),type="l") |
||
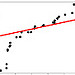 quantile-quantile plot quantile-quantile plot |
qqplot(runif(50),rnorm(50)) lines(c(-9,9), c(-9,9), col="red") |
|||
| axis label | plot(1:20, (1:20)^2, xlab="x", ylab="x squared") | |||
| axis limits | plot(1:20, (1:20)^2, xlab="x", ylab="x squared", ylim=c(-200,500)) | |||
| logarithmic y-axis | x = 0:20 plot(x,x^2,log="y",type="l") lines(x,x^3,col="blue") lines(x,x^4,col="green") lines(x,x^5,col="red") |
x = range(0, 20) for i in [2,3,4,5]: y.append([j**i for j in x]) for i in [0,1,2,3]: semilogy(x, y[i]) |
||
| trivariate charts | ||||
| matlab | r | matplotlib | ||
| 3d scatter plot | ||||
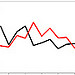 additional data set additional data set |
plot(1:20, rnorm(20), type="l") lines(1:20, rnorm(20), col="red") |
|||
| bubble chart | ||||
| surface plot | ||||
| __________________________________________ | __________________________________________ | __________________________________________ | __________________________________________ | |
General Footnotes
version used
The version of software used to check the examples in the reference sheet.
implicit prologue
Code which examples in the sheet assume to have already been executed.
get version
How to determine the version of an installation.
command line repl
How to launch a command line read-eval-print loop for the language.
r:
R installations come with a clickable GUI REPL.
interpreter
How to invoke the interpreter on a script.
compiler
How to compile an executable.
statement separator
How statements are separated.
octave:
Use a backslash to escape a newline and continue a statement on the following line. MATLAB, in contrast, uses three periods: '…' to continue a statement on the following line.
block delimiters
Punctuation or keywwords which define blocks.
fortran:
The list of keywords is not exhaustive.
octave:
The list of keywords which define blocks is not exhaustive. Blocks are also defined by
- switch, case, otherwise, endswitch
- unwind_protect, unwind_protect_cleanup, end_unwind_protect
- try, catch, end_try_catch
assignment
r:
Traditionally <- was used in R for assignment. Using an = for assignment was introduced in version 1.4.0 sometime before 2002. -> can also be used for assignment:
3 -> x
compound assignment operators: arithmetic, string, logical
The compound assignment operators.
increment and decrement operator
The operator for incrementing the value in a variable; the operator for decrementing the value in a variable.
to-end-of-line comment
Character used to start a comment that goes to the end of the line.
null
octave:
NA can be used for missing numerical values. Using a comparison operator on it always returns false, including NA == NA. Using a logical operator on NA raises an error.
r:
Comparison operators return NA when one of the arguments is NA. In particular NA == NA is NA. When acting on values that might be NA, the logical operators observe the rules of ternary logic, treating NA is the unknown value.
null test
How to test if a value is null.
undefined variable access
What happens when a variable which hasn't been declared or defined is accessed.
variable types
The types which are available for variable declaration.
variable declaration
How to declare the type of a variable.
are identifiers case sensitive
Are identifiers case sensitive?
Arithmetic and Logic Footnotes
true and false
The boolean literals.
octave:
true and false are functions which return matrices of ones and zeros of type logical. If no arguments are specified they return single entry matrices. If one argument is provided, a square matrix is returned. If two arguments are provided, they are the row and column dimensions.
falsehoods
Values which evaluate to false in a conditional test.
octave:
When used in a conditional, matrices evaluate to false unless they are nonempty and all their entries evaluate to true. Because strings are matrices of characters, an empty string ('' or "") will evaluate to false. Most other strings will evaluate to true, but it is possible to create a nonempty string which evaluates to false by inserting a null character; e.g. "false\000".
r:
When used in a conditional, a vector evaluates to the boolean value of its first entry. Using a vector with more than one entry in a conditional results in a warning message. Using an empty vector in a conditional, c() or NULL, raises an error.
logical operators
The boolean operators.
octave:
Note that MATLAB does not use the exclamation point '!' for negation.
&& and || are short circuit logical operators.
conditional expression
A conditional expression.
convert from string, to string
How to convert strings to numbers and vice versa.
comparison operators
The comparison operators.
octave:
Note that MATLAB does not use '!=' for an inequality test.
arithmetic operators
The arithmetic operators.
octave:
^ is a synonym for **.
mod is a function and not an infix operator. mod returns a positive value if the first argument is positive, whereas rem returns a negative value.
r:
^ is a synonym for **.
integer division
How to compute the quotient of two integers.
float division
How to perform float division, even if the arguments are integers.
arithmetic functions
Some standard arithmetic functions.
arithmetic truncation
Ways of converting a float to a nearby integer.
arithmetic decomposition
Ways of decomposing numbers into a simpler type of number.
closure of integers under division
The data type of an expression which divides two integers.
integer overflow
What happens when an expression evaluates to an integer which is too big to be represented.
float overflow
What happens when an expression evaluates to a float which is too big to be represented.
float limits
The machine epsilon; the largest representable float and the smallest (i.e. closest to negative infinity) representable float.
1/0
The result of division by zero.
sqrt(-2)
The result of taking the square root of a negative number.
complex numbers
Literals for complex numbers.
random integer
How to generate a random integer from a uniform distribution.
random float
How to generate a random float from a uniform distribution.
setting seed
How to set the seed used by the random number generator.
result of not seeding
What happens if no seed was set and a random number is generated.
String Footnotes
literal
The syntax for a string literal.
newline in literal
Can a newline be included in a string literal? Equivalently, can a string literal span more than one line of source code?
literal escapes
Escape sequences for including special characters in string literals.
character access
How to get the character in a string at a given index.
chr and ord
How to convert an ASCII code to a character; how to convert a character to its ASCII code.
length
How to get the number of characters in a string.
concatenate
How to concatenate strings.
replicate
How to create a string which consists of a character of substring repeated a fixed number of times.
index of substring
How to get the index of first occurrence of a substring.
extract substring
How to get the substring at a given index.
split
How to split a string into an array of substrings. In the original string the substrings must be separated by a character, string, or regex pattern which will not appear in the array of substrings.
The split operation can be used to extract the fields from a field delimited record of data.
join
How to join an array of substrings into single string. The substrings can be separated by a specified character or string.
Joining is the inverse of splitting.
trim
How to remove whitespace from the beginning and the end of a string.
Trimming is often performed on user provided input.
case manipulation
How to put a string into all caps. How to put a string into all lower case letters. How to capitalize the first letter of a string.
sprintf
How to create a string using a printf style format.
fortran:
Fortran format strings use these expressions:
| A | character |
| Dwidth.precision | double in scientific notation |
| Ewidth.precision | real in scientific notation |
| Fwidth.precision | real in fixed point notation |
| Iwidth | integer |
| X | space |
| nX | repeat following format expression n times |
| / | newline |
width and precision are integers. width is the field width in characters. Other characters in the format string are ignored.
regex test
How to test whether a string matches a regular expression.
regex substitution
How to replace all substring which match a pattern with a specified string; how to replace the first substring which matches a pattern with a specified string.
Date and Time Footnotes
current date/time
How to get the current date and time.
fortran:
The Fortran 95 standard specifies two date functions: system_clock() and date_and_time().
system_clock() returns the number of clock ticks since an unspecified time. The number of ticks per second can be specified as an argument. Since the start time is unspecified it is difficult to use this function in a portable way. date_and_time() can be used to decompose the return value of system_clock() into year, month, day, hour, minute, and second.
GNU Fortran provides functions similar to functions in the C standard library.
r:
Sys.time() returns a value of type POSIXct.
date/time type
The data type used to hold a combined date and time value.
date/time difference type
The data type used to hold the difference between two date/time types.
get date parts
How to get the year, the month as an integer from 1 through 12, and the day of the month from a date/time value.
fortran:
ltime() gets the parts that correspond to the local time zone. gmtime() can be used to get the parts that correspond to the UTC time zone.
get time parts
How to get the hour as an integer from 0 through 23, the minute, and the second from a date/time value.
fortran:
ltime() gets the parts that correspond to the local time zone. gmtime() can be used to get the parts that correspond to the UTC time zone.
build date/time from parts
How to build a date/time value from the year, month, day, hour, minute, and second as integers.
convert to string
How to convert a date value to a string using the default format for the locale.
strptime
How to parse a date/time value from a string in the manner of strptime from the C standard library.
strftime
How to write a date/time value to a string in the manner of strftime from the C standard library.
Multidimensional Array Footnotes
Arrays map integers to arbitrary values. The arrays supported by the languages in this reference sheet are homogeneous, which means that the values in the codomain of the array must all be of the same type.
The languages in this sheet all support multidimensional arrays. A multidimensional array maps tuples of integers to values. All tuples which can be used as indices in a multidimensional array are of the same length and this length is the dimension of the array.
Arrays use contiguous regions of memory to store their values. Thus, an array with an element at index 1 and index 10 must allocate space for elements at indices 2 through 9, even if values are not explicitly set or needed. The shape of a multidimensional array can be expressed by a tuple of positive integers with the same length as the dimension of the array.
Arrays provide constant time access when looking up values by their indices.
A vector is a one dimensional array which supports these operations:
- addition on vectors of the same length
- scalar multiplication
- a dot product
- a norm
The languages in this reference sheet provide the above operations for all one dimensional arrays which contain numeric values.
NumPy adds the homogeneous ndarray type to the native Python list. A Python list is nonhomogeneous and one dimensional, but because they can contain lists as values they can be used to hold multidimensional data. Python lists are described in the Python reference sheet.
array literal
octave:
An array in Octave is in fact a 1 x n matrix.
r:
c(1,2,3) is a vector and array(c(1,2,3)) is a one dimensional array. The documentation says that some functions may treat the two objects differently. In the absence of knowing what those differences are it seems best to use the vector.
2d array literal
3d array literal
must arrays be homogeneous
Can an array be created with elements of different type?
octave:
The array literal
[1,'foo',3]
will create an array with 5 elements of class char.
r:
The array literal
c(1,'foo',3)
will create an array of 3 elements of class character, which is the R string type.
array data types
What data types are permitted in arrays.
octave:
Arrays in Octave can only contain numeric elements. This follows from the fact that Octave "arrays" are in fact 1 x n matrices.
Array literals can have a nested structure, but Octave will flatten them. The following literals create the same array:
[ 1 2 3 [ 4 5 6] ]
[ 1 2 3 4 5 6 ]
Logical values can be put into an array because true and false are synonyms for 1 and 0. Thus the following literals create the same arrays:
[ true false false ]
[ 1 0 0 ]
If a string is encountered in an array literal, the string is treated as an array of ASCII values and it is concatenated with other ASCII values to produce as string. The following literals all create the same string:
[ 'foo', 98, 97, 114]
[ 'foo', 'bar' ]
'foobar'
If the other numeric values in an array literal that includes a string are not integer values that fit into a ASCII byte, then they are converted to byte sized values.
r:
Array literals can have a nested structure, but R will flatten them. The following literals produce the same array of 6 elements:
c(1,2,3,c(4,5,6))
c(1,2,3,4,5,6)
If an array literal contains a mixture of booleans and numbers, then the boolean literals will be converted to 1 (for TRUE and T) and 0 (for FALSE and F).
If an array literal contains strings and either booleans or numbers, then the booleans and numbers will be converted to their string representations. For the booleans the string representations are "TRUE'" and "FALSE".
array element access
index of array element
array length
array concatenation
map
filter
reduce
Tuple, Dictionary, and Sequence Footnotes
| homogeneous array | vector | tuple | record | map | |
|---|---|---|---|---|---|
| NumPy | list | vector | tuple | dict | dict |
| Octave | rank 1 matrix | rank 1 matrix | cell array | struct | |
| R | vector | vector | list | list |
tuple literal
How to create a tuple, which we define as a fixed length, inhomogeneous list.
tuple element access
How to access an element of a tuple.
tuple length
How to get the number of elements in a tuple.
dictionary literal
The syntax for a dictionary literal.
dictionary lookup
How to use a key to lookup a value in a dictionary.
range
Function Foontotes
definition
invocation
function value
Execution Control Footnotes
if
How to write a branch statement.
while
How to write a conditional loop.
for
How to write a C-style for statement.
break/continue
How to break out of a loop. How to jump to the next iteration of a loop.
fortran:
Fortran has a continue statement which is a no-op statement used as a target for goto statements.
Here is an example of using exit to terminate what would otherwise be an infinite loop:
n = 1
do
if (n > 10) exit
write(*, *) n
n = n + 1
end do
Labels can be provided for nested do loops. The labels can be provided as arguments to exit and cycle:
foo: do
bar: do n = 1, 10, 1
write(*,*) n
exit foo
end do bar
end do foo
raise exception
How to raise an exception.
handle exception
How to handle an exception.
finally block
How to write code that executes even if an exception is raised.
Environment and I/O Foontotes
Library and Module Footnotes
load library
How to load a library.
list loaded libraries
Show the list of libraries which have been loaded.
library search path
The list of directories the interpreter will search looking for a library to load.
source file
How to source a file.
r:
When sourcing a file, the suffix if any must be specified, unlike when loading library. Also, a library may contain a shared object, but a sourced file must consist of just R source code.
install package
How to install a package.
list installed packages
How to list the packages which have been installed.
Reflection Footnotes
data type
How to get the data type of a value.
attributes
How to get the attributes for an object.
methods
How to get the methods for an object.
variables in scope
How to list the variables in scope.
undefine variable
How to undefine a variable.
eval
How to interpret a string as source code and execute it.
function documentation
How to get the documentation for a function.
list library functions
How to list the functions and other definitions in a library.
search documentation
How to search the documentation by keyword.
Vector Footnotes
vector literal
element-wise arithmetic operators
scalar multiplication
dot product
cross product
norms
octave:
The norm function returns the p-norm, where the second argument is p. If no second argument is provided, the 2-norm is returned.
Matrix Footnotes
literal or constructor
Literal syntax or constructor for creating a matrix.
The elements of a matrix must be specified in a linear order. If the elements of each row of the matrix are adjacent to other elements of the same row in the linear order we say the order is row contiguous. If the elements of each column are adjacent to other elements of the same column we say the order is column contiguous.
octave:
Square brackets are used for matrix literals. Semicolons are used to separate rows, and commas separate row elements. Optionally, newlines can be used to separate rows and whitespace to separate row elements.
r:
Matrices are created by passing a vector containing all of the elements, as well as the number of rows and columns, to the matrix constructor.
If there are not enough elements in the data vector, the values will be recycled. If there are too many extra values will be ignored. However, the number of elements in the data vector must be a factor or a multiple of the number of elements in the final matrix or an error results.
When consuming the elements in the data vector, R will normally fill by column. To change this behavior pass a byrow=T argument to the matrix constructor:
A = matrix(c(1,2,3,4),nrow=2,byrow=T)
dimensions
How to get the dimensions of a matrix.
element access
How to access an element of a matrix. All languages described here follow the convention from mathematics of specifying the row index before the column index.
octave:
Rows and columns are indexed from one.
r:
Rows and columns are indexed from one.
row access
How to access a row.
column access
How to access a column.
submatrix access
How to access a submatrix.
scalar multiplication
How to multiply a matrix by a scalar.
element-wise operators
Operators which act on two identically sized matrices element by element. Note that element-wise multiplication of two matrices is used less frequently in mathematics than matrix multiplication.
from numpy import array
matrix(array(A) * array(B))
matrix(array(A) / array(B))
multiplication
How to multiply matrices. Matrix multiplication should not be confused with element-wise multiplication of matrices. Matrix multiplication in non-commutative and only requires that the number of columns of the matrix on the left match the number of rows of the matrix. Element-wise multiplication, by contrast, is commutative and requires that the dimensions of the two matrices be equal.
kronecker product
The Kronecker product is a non-commutative operation defined on any two matrices. If A is m x n and B is p x q, then the Kronecker product is a matrix with dimensions mp x nq.
comparison
How to test two matrices for equality.
octave:
== and != perform entry-wise comparison. The result of using either operator on two matrices is a matrix of boolean values.
~= is a synonym for !=.
r:
== and != perform entry-wise comparison. The result of using either operator on two matrices is a matrix of boolean values.
norms
How to compute the 1-norm, the 2-norm, the infinity norm, and the frobenius norm.
octave:
norm(A) is the same as norm(A,2).
Statistics Footnotes
A statistic is a single number which summarizes a population of data. The most familiar example is the mean or average. Statistics defined for discrete populations can often be meaningfully extended to continuous distributions by replacing summations with integration.
An important class of statistics are the nth moments. The nth moment $\mu'_n$ of a population of k values xi with mean μ is:
(1)The nth central moment μn of the same population is:
(2)first moment statistics
The sum and the mean.
The mean is the first moment. It is one definition of the center of the population. The median and the mode are also used to define the center. In most populations they will be close to but not identical to the mean.
second moment statistics
The variance and the standard deviation. The variance is the second central moment. It is a measure of the spread or width of the population.
The standard deviation is the square root of the variance. It is also a measurement of population spread. The standard deviation has the same units of measurement as the data in the population.
second moment statistics for samples
The sample variance and sample standard deviation.
skewness
The skewness of a population.
The skewness measures the asymmetrically of the population. The skewness will be negative, positive, or zero when the population is more spread out on the left, more spread out on the right, or similarly spread out on both sides, respectively.
The skewness can be calculated from the third moment and the standard deviation:
(3)When estimating the population skewness from a sample a correction factor is often used, yielding the sample skewness:
(4)octave and matlab:
Octave uses the sample standard deviation to compute skewness. This behavior is different from Matlab and should possibly be regarded as a bug.
Matlab, but not Octave, will take a flag as a second parameter. When set to zero Matlab returns the sample skewness:
skewness(x, 0)
numpy:
Set the named parameter bias to False to get the sample skewness:
stats.skew(x, bias=False)
kurtosis
The kurtosis of a population.
The formula for kurtosis is:
(5)When kurtosis is negative the sides of a distribution tend to be more convex than when the kurtosis is is positive. A negative kurtosis distribution tends to have a wide, flat peak and narrow tails. Such a distribution is called platykurtic. A positive kurtosis distribution tends to have a narrow, sharp peak and long tails. Such a distribution is called leptokurtic.
The fourth standardized moment is
(6)The fourth standardized moment is sometimes taken as the definition of kurtosis in older literature. The reason the modern definition is preferred is because it assigns the normal distribution a kurtosis of zero.
octave:
Octave uses the sample standard deviation when computing kurtosis. This should probably be regarded as a bug.
r:
R uses the older fourth standardized moment definition of kurtosis.
nth moment and nth central moment
How to compute the nth moment (also called the nth absolute moment) and the nth central moment for arbitrary n.
mode
The mode is the most common value in the sample.
The mode is a measure of central tendency like the mean and the median. A problem with the mean is that it can produce values not found in the data. For example the mean number of persons in an American household was 2.6 in 2009.
The mode might not be unique. If there are two modes the sample is said to be bimodal, and in general if there is more than one mode the sample is said to be multimodal.
quantile statistics
If the data is sorted from smallest to largest, the minimum is the first value, the median is the middle value, and the maximum is the last value. If there are an even number of data points, the median is the average of the middle two points.
The median divides the population into two halves. When the population is divided into four parts the division markers are called the first, second, and third quartile. When the population is divided into a hundred the division markers are called percentiles. If the population is divided into nparts the markers are called the 1st, 2nd, …, (n-1)th n-quantile.
linear regression y = ax + b
How to get the slope a and intercept b for a line which best approximates the data. How to get the residuals.
If there are more than two data points, then the system is overdetermined and in general there is no solution for the slope and the intercept. Linear regression looks for line that fits the points as best as possible. The least squares solution is the line that minimizes the sum of the square of the distances of the points from the line.
The residuals are the difference between the actual values of y and the calculated values using ax + b. The norm of the residuals can be used as a measure of the goodness of fit.
bivariate statistics
The correlation and the covariance.
The correlation is a number from -1 to 1. It is a measure of the linearity of the data, with values of -1 and 1 representing indicating a perfectly linear relationship. When the correlation is positive the quantities tend to increase together and when the correlation is negative one quantity will tend to increase as the other decreases.
A variable can be completely dependent on another and yet the two variables can have zero correlation. This happens for Y = X2 where uniform X on the interval [-1, 1]. Anscombe's quartet gives four examples of data sets each with the same fairly high correlation 0.816 and yet which show significant qualitative differences when plotted.
The covariance is defined by
(7)The correlation is the normalized version of the covariance. It is defined by
(8)Distribution Footnotes
A distribution density function f(x) is a non-negative function which, when integrated over its entire domain is equal to one. The distributions described in this sheet have as their domain the real numbers. The support of a distribution is the part of the domain on which the density function is non-zero.
A distribution density function can be used to describe the values one is likely to see when drawing an example from a population. Values in areas where the density function is large are more likely than values in areas where the density function is small. Values where there density function is zero do not occur. Thus it can be useful to plot the density function.
To derive probabilities from a density function one must integrate or use the associated cumulative density function
(9)which gives the probability of seeing a value less than or equal to x. As probabilities are non-negative and no greater than one, F is a function from (-∞, ∞) to [0,1]. The inverse of F is called the inverse cumulative distribution function or the quantile function for the distribution.
For each distribution statistical software will generally provide four functions: the density, the cumulative distribution, the quantile, and a function which returns random numbers in frequencies that match the distribution. If the software does not provide a random number generating function for the distribution, the quantile function can be composed with the built-in random number generator that most languages have as long as it returns uniformly distributed floats from the interval [0, 1].
| density probability density probability mass |
cumulative density cumulative distribution distribution |
inverse cumulative density inverse cumulative distribution quantile percentile percent point |
random variate |
Discrete distributions such as the binomial and the poisson do not have density functions in the normal sense. Instead they have probability mass functions which assign probabilities which sum up to one to the integers. In R warnings will be given if non integer values are provided to the mass functions dbinom and dpoiss.
The cumulative distribution function of a discrete distribution can still be defined on the reals. Such a function is constant except at the integers where it may have jump discontinuities.
Most well known distributions are in fact parametrized families of distributions. The following table lists some of them with their parameters and properties:
| distribution | parameters | support | density f(x) | mean | variance | excel function |
|---|---|---|---|---|---|---|
| binomial | B(n,p) | {0,1,…,n} | $\frac{n!}{x!(n-x)!} p^x(1-p)^{n-x}$ | np | np(1-p) | BINOMDIST(x,n,p,FALSE) BINOMDIST(x,n,p,TRUE) BINOM.INV(n, p, α) BINOM.INV(n, p, RAND()) |
| poisson | Pois(λ) | {0,1,2,…} | $\frac{\mu^x e^{-\mu}}{x!}$ | λ | λ | POISSON(x, λ, FALSE) POISSON(x, λ, TRUE) none none |
| normal | N(μ, σ) | (-∞,∞) | $\frac{1}{\sqrt{2\pi \sigma}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$ | μ | σ2 | NORMDIST(x, μ, σ, FALSE) NORMDIST(x, μ, σ, TRUE) NORMINV(α, μ, σ) NORMINV(RAND(), μ, σ) |
| gamma | Γ(k, θ) | [0,∞) | $x^{k-1}\frac{exp(\frac{-x}{\theta})}{\Gamma(k) \theta^k}$ | kθ | kθ2 | GAMMADIST(x, k, θ, FALSE) GAMMADIST(x, k, θ, TRUE) GAMMAINV(α, k, θ) GAMMAINV(RAND(), k, θ) |
| exponential | Exp(λ) | [0, ∞) | $\lambda e^{-\lambda x}$ | λ-1 | λ-2 | EXPON.DIST(x, λ, FALSE) EXPON.DIST(x, λ, TRUE) GAMMAINV(y, 1, 1/λ) GAMMAINV(RAND(), 1, 1/λ) |
| chi-squared | Χ2(ν) | [0, ∞) | $\frac{1}{2^{k/2}\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$ | ν | 2ν | CHISQ.DIST(x, ν, FALSE) CHISQ.DIST(x, ν, TRUE) CHISQ.INV(y, ν) CHISQ.INV(RAND(), ν) |
| beta | Be(α, β) | [0, 1] | $\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}$ | $\frac{\alpha}{\alpha + \beta}$ | $\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$ | BETADIST(x, α, β, FALSE) BETADIST(x, α, β, TRUE) BETAINV(p, α, β) BETAINV(RAND(), α, β) |
| uniform | U(a, b) | [a, b] | $\frac{1}{b-a}$ | $\frac{a+b}{2}$ | $\frac{(b-a)^2}{12}$ | 1/(b-a) (x-a)/(b-a) α * (b-a) + a RAND()*(b-a) + a |
| Student's t | t(ν) | (-∞,∞) | $\frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu \pi} \Gamma(\frac{\nu}{2})} (1 + \frac{x^2}{\nu})^{-\frac{\nu+1}{2}}$ | $\begin{cases} 0 & \nu > 1 \\ \text{undefined} & \text{otherwise} \end{cases}$ | $\begin{cases} \frac{\nu}{\nu - 2} & \nu > 2 \\ \infty & 1 < \nu \le 2 \\ \text{undefined} & \text{otherwise} \end{cases}$ | T.DIST(x, ν, FALSE) T.DIST(x, ν, TRUE) T.INV(α, ν) T.INV(RAND(), ν) |
| Snedecor's F | F(d1, d2) | [0, ∞) | $\frac{\sqrt{\frac{(d_1 x)^{d_1} d_2^{d_2}}{(d_1 x + d_2)^{d_1+d_2}}}}{x B(d_1, d_2)}$ | $\frac{d_2}{d_2 - 2}$ for d2 > 2 | F.DIST(x, d1, d2, FALSE) F.DIST(x, d1, d2, TRUE) F.INV(α, d1, d2) F.INV(RAND(), d1, d2) |
|
| ________ | _____________________ |
The information entropy of a continuous distribution with density f(x) is defined as:
(10)In Bayesian analysis the distribution with the greatest entropy, subject to the known facts about the distribution, is called the maximum entropy probability distribution. It is considered the best distribution for modeling the current state of knowledge.
binomial
The probability mass, cumulative distribution, quantile, and random number generating functions for the binomial distribution.
The binomial distribution is a discrete distribution. It models the number of successful trails when n is the number of trials and p is the chance of success for each trial. An example is the number of heads when flipping a coin 100 times. If the coin is fair then p is 0.50.
numpy:
Random numbers in a binomial distribution can also be generated with:
np.random.binomial(n, p)
poisson
The probability mass, cumulative distribution, quantile, and random number generating functions for the binomial distribution.
The poisson distribution is a discrete distribution. It is described by a parameter lam which is the mean value for the distribution. The poisson distribution is used to model events which happen at a specified average rate and independently of each other. Under these circumstances the time between successive events will be described by an exponential distribution and the events are said to be described by a poisson process.
numpy:
Random numbers in a poisson distribution can also be generated with:
np.random.poisson(lam, size=1)
normal
The probability density, cumulative distribution, quantile, and random number generating functions for the uniform distribution.
The parameters are the mean μ and the standard deviation σ. The standard normal distribution has μ of 0 and σ of 1.
The normal distribution is the maximum entropy distribution for a given mean and variance. According to the central limit theorem, if {X1, …, Xn} are any independent and identically distributed random variables with mean μ and variance σ2, then Sn := Σ Xi / n converges to a normal distribution with mean μ and variance σ2/n.
numpy:
Random numbers in a normal distribution can also be generated with:
np.random.randn()
gamma
The probability density, cumulative distribution, quantile, and random number generating functions for the gamma distribution.
The parameter k is called the shape parameter and θ is called the scale parameter. The rate of the distribution is β = 1/θ.
If Xi are n independent random variables with Γ(ki, θ) distribution, then Σ Xi has distribution Γ(Σ ki, θ).
If X has Γ(k, θ) distribution, then αX has Γ(k, αθ) distribution.
exponential
The probability density, cumulative distribution, quantile, and random number generating functions for the exponential distribution.
chi-squared
The probability density, cumulative distribution, quantile, and random number generating functions for the chi-squared distribution.
beta
The probability density, cumulative distribution, quantile, and random number generating functions for the beta distribution.
uniform
The probability density, cumulative distribution, quantile, and random number generating functions for the uniform distribution.
The uniform distribution is described by the parameters a and b which delimit the interval on which the density function is nonzero.
The uniform distribution is maximum entropy probability distribution with support [a, b].
Consider the uniform distribution on [0, b]. Suppose that we take k samples from it, and m is the largest of the samples. The minimum variance unbiased estimator for b is
(11)octave, r, numpy:
a and b are optional parameters and default to 0 and 1 respectively.
Student's t
The probability density, cumulative distribution, quantile, and random number generating functions for Student's t distribution.
Snedecor's F
The probability density, cumulative distribution, quantile, and random number generating functions for Snedecor's F distribution.
Data Set Footnotes
A data set is essentially an in memory database table. Data sets are called data frames in R. Pandas is a Python library which implements a data set.
construct from arrays
How to construct a data set from a set of arrays representing the columns.
view in spreadsheet
How to view and edit the data set in a spreadsheet.
list column names
How to show the names of the columns.
attach column names
How to make column name a variable in the current scope which refers to the column as an array.
r:
Each column of the data set is copies into a variable named after the column containing the column as a vector. Modifying the data in the variable does not alter the original data set.
detach column names
How to remove attached column names from the current scope.
column access
How to access a column in a data set.
row access
How to access a row in a data set.
r:
people[1,] returns the 1st row from the data set people as a new data set with one row. This can be converted to a list using the function as.list. There is often no need because lists and one row data sets have nearly the same behavior.
access sub data set
How to select a subset of the rows and a subset of the columns.
access datum
How to access a single datum in a data set; i.e. the value in a column of a single row.
sort rows of data set
How to sort the rows in a data set according to the values in a specified column.
sort rows of data set
How to sort the rows in descending order according to the values in a specified column.
map data set
How to apply a mapping transformation to the rows of a data set.
filter data set
How to select the rows of a data set that satisfy a predicate.
load from csv
Load a data set from a CSV file.
save as csv
Save a data set to a CSV file.
show built-in data sets
Show the built-in data sets.
load built-in data set
Load one of the built-in data sets.
Univariate Chart Footnotes
A univariate chart can be used to display a list or array of numerical values. Univariate data can be displayed in a table with a single column or two columns if each numerical value is given a name. A multivariate chart, by contrast, is used to display a list or array of tuples of numerical values.
In order for a list of numerical values to be meaningfully displayed in a univariate chart, it must be meaningful to perform comparisons (<, >, =) on the values. Hence the values should have the same unit of measurement.
vertical bar chart
A chart which represents values with rectangular bars which line up on the bottom. It is a deceptive practice for the bottom not to represent zero, even if a y-axis with labelled tick marks or grid lines is provided. A cut in the vertical axis and one of the bars may be desirable if the cut value is a large outlier. Putting such a cut all of the bars near the bottom is a deceptive practice similar not taking to the base of the bars to be zero, however.
Another bad practice is the 3D bar chart. In such a chart heights are represented by the height of what appear to be three dimensional blocks. Such charts impress an undiscriminating audience but make it more difficult to make a visual comparison of the charted quantities.
horizontal bar chart
A bar chart in which zero is the y-axis and the bars extend to the right.
pie chart
A bar chart displays values using the areas of circular sectors or equivalently, the lengths of the arcs of those sectors. A pie chart implies that the values are percentages of a whole. The viewer is likely to make an assumption about what the whole circle represents. Thus, using a pie chart to show the revenue of some companies in a line of business could be regarded as deceptive if there are other companies in the same line of business which are left out. The viewer may mistakenly assume the whole circle represents the total market.
If two values are close in value, people cannot determine visually which of the corresponding sectors in a pie chart is larger without the aid of a protractor. For this reason many consider bar charts superior to pie charts.
Many software packages make 3D versions of pie charts which communicate no additional information and in fact make it harder to interpret the data.
stacked dot chart
A chart which communicates values by means of stacks of dots. A dot chart is equivalent to a bar chart but emphasizes that the quantities are small, integral values.
There is a single dot variation of the dot chart in which only the topmost dot is drawn. The single dot variation will draw the dot on a line; it doesn't imply that the represented quantity is an integer.
stem-and-leaf plot
histogram
box-and-whisker plot
set chart title
Bivariate Chart Footnotes
stacked bar chart
Trivariate Chart Footnotes
Fortran
The GNU Fortran Compiler
Fortran 77 Tutorial
Fortran 90 Tutorial
Fortran Standards Documents
BLAS: A Quick Reference Guide (pdf)
Modern Fortran compilers support two source code formats: the traditional fixed format and the free format introduced with Fortran 90.
If a Fortran source file has a .f suffix, the gfortran compiler expects the code to have fixed format. If the suffix is .f90 or .f95 it expects free format code. Emacs is also suffix aware and provides fortran-mode and f90-mode for fixed format and free format code respectively.
Here is an example of fixed format code:
C Hello World
* in Fortran 77
program hello
10000 write(*,*) 'Hello,'
+ , ' World!'
end program hello
This first column can contain a 'C', 'c', or '*' to indicate the line is a comment.
Columns 1 through 5 can contain an optional statement label. A statement label consists of digits. The statement label may contain leading zeros which are ignored. A statement label cannot consist entirely of zeros.
If column 6 contains a non-space character and columns 1 through 5 are blank, then the line is treated as a continuation of the previous line. The continuation character is not itself part of the statement, so any non-space character can be used, but '+' is a common choice.
Columns 7 through 72 contain the statement.
Columns 73 through 80 can contain optional sequence numbers. They were formerly used to help keep punch cards in the correct order.
Here is an example of free format code:
! Hello World in Fortran 90
program hello
write(*,*) 'Hello,' &
, ' World!'
end program hello
There are no special columns in free format code. There is no limit on the length of lines or statements. If it is desirable to split a statement up over multiple lines, the '&' character can be used to indicate the statement continues on the following line.
MATLAB
Octave Manual
MATLAB Documentation
gnuplot Documentation
Differences between Octave and MATLAB
Octave-Forge Packages
The basic data type of MATLAB is a matrix of floats. There is no distinction between a scalar and a 1x1 matrix, and functions that work on scalars typically work on matrices as well by performing the scalar function on each entry in the matrix and returning the resultings in a matrix with the same dimensions. Operators such as the logical operators ('&' '|' '!'), comparison operators ('==', '!=', '<', '>'), and arithmetic operators ('+', '-') all work this way. However the multiplication '*' and division '/' operators perform matrix multiplication and matrix division, respectively. The '.*' and '.*' operators are available if entry-wise multiplication or division is desired.
Floats are by default double precision; single precision can be specified with the single constructor. MATLAB has convenient matrix literal notation: commas or spaces can be used to separate row entries, and semicolons or newlines can be used to separate rows.
Arrays and vectors are implemented as single-row (1xn) matrices. As a result an n-element vector must be transposed before it can be multiplied on the right of a mxn matrix.
Numeric literals that lack a decimal point such as 17 and -34 create floats, in contrast to most other programming languages. To create an integer, an integer constructor which specifies the size such as int8 and uint16 must be used. Matrices of integers are supported, but the entries in a given matrix must all have the same numeric type.
Strings are implemented as single-row (1xn) matrices of characters, and as a result matrices cannot contain strings. If a string is put in matrix literal, each character in the string becomes an entry in the resulting matrix. This is consistent with how matrices are treated if they are nested inside another matrix. The following literals all yield the same string or 1xn matrix of characters:
'foo'
[ 'f' 'o' 'o' ]
[ 'foo' ]
[ [ 'f' 'o' 'o' ] ]
true and false are functions which return matrices of ones and zeros. The ones and zeros have type logical instead of double, which is created by the literals 1 and 0. Other than having a different class, the 0 and 1 of type logical behave the same as the 0 and 1 of type double.
MATLAB has a tuple type (in MATLAB terminology, a cell array) which can be used to hold multiple strings. It can also hold values with different types.
Octave is a free, open source application for floating point and matrix computations which can interface with numerical routines implemented in C or Fortran. Octave implements the core MATLAB language, and as a result MATLAB scripts will usually run under Octave. Octave scripts are less likely to run under MATLAB because of extensions which Octave is made to the core language.. Octave's plotting functions use gnuplot.
R
An Introduction to R
The Comprehensive R Archive Network
R is an application for statistical analysis. It is a free, open source implementation of the S programming language developed at Bell Labs.
The basic data types of R are vectors of floats, vectors of strings, and vectors of booleans. There is no distinction between a scalar and a vector with one entry in it, and functions and operators which accept a scalar argument will typically accept a vector argument, returning a vector of the same size with the scalar operation performed on each the entries of the original vector.
The scalars in a vector must all be of the same type, but R also provides a list data type which can be used as a tuple (entries accessed by index) or a record (entries accessed by name).
In addition R provides a data frame type which is a list (in R terminology) of vectors all of the same length. Data frames are equivalent to the data sets of other statistical analysis packages.
NumPy
NumPy and SciPy Documentation
matplotlib intro
NumPy for Matlab Users
History
Fortran History
The initial Fortran compiler was released for the IBM 704 in 1957. It was followed by the Fortran II compiler in 1958 which added support for user defined functions and subroutines.
In 1962 IBM released Fortran IV, which was tweaked to make it easier to write portable programs. IBM released Fortran IV compilers for the IBM 7090, 7094, and IBM's first supercomputer, the 7030. Fortrran IV became an ANSI in 1966.
In 1977 the Fortran standard was updated to add block IF statements and the CHARACTER data type. Before the CHARACTER data type, string data was handled using Hollerith constants. An example of a Hollerith constant for 'ABC' is 3HABC. The three indicates the number of characters. The largest number that could be used in a Hollerith constant depended upon the machine architecture and in particular how many characters could be stored in an integer data type.
In 1990 the Fortran standard was updated, adding free format text for source code as an option to the traditional fixed format. The fixed format is a relic from when programs were entered by punching them into punch cards.
MATLAB History
In the 1970s the Argonne National Laboratory wrote some high quality Fortran libraries for matrix computations, starting with EISPACK in 1973. Cleve Moler, a professor at the University of New Mexico, developed the scripting language MATLAB (Matrix Laboratory) in the late 1970s so that students could use these libraries without knowing Fortran. MATLAB was initially free, but it was reimplemented in C and released as a commercial product in 1984.
Version 1.0 of Octave was release in 1994 under the GNU license.
R History
A Brief History of S Becker 1994
S, a language for doing work in statistics, was developed by John Chambers and others at Bell Labs in 1976. Originally it ran on the GCOS operating system. It was ported to Unix in 1979, and distributed outside of Bell Labs with source in 1981. SAS, by comparison, was initially released in 1971 for IBM mainframes, and was ported to other systems such as VMS in the early 1980s. Both S and SAS were initially implemented in Fortran. The source code for S in particular was run through the M4 and then the Ratfor preprocessors before compilation by the Fortran compiler.
The S language was revised in 1988. Functions were added to the language, which previously only had macros. The functions could be stored in variables and higher order functions such as apply were added. Data frames were also added and multiple dispatch was implemented for the print function.
R is a GNU version of S. The first stable production version was released in 2000.
NumPy History
Numeric was the predecessor of NumPy. It appeared in 1995. Several libraries written on top of Numeric merged to become SciPy in 2001.
In 2005 the code for Numeric was refactored to make it more maintainable, in the hope of eventually getting it into the Python standard library. It was renamed NumPy. It incorporated some of the features from a competing package called numarray.